Carga Elétrica – Aula completa PDF

Segundo Benjamim Franklin existem dois tipos de cargas eléctricas, positivas e negativas. As cargas do mesmo sinal repelem-se, e as cargas de sinais contrários atraem-se. A lei do inverso do quadrado (lei quantitativa), para as interacções eléctricas, foi confirmada experimentalmente por Charles Coulomb (1736-1806), usando uma balança de torção.

Após passar algumas vezes um pente de plástico pelo cabelo, verifica-se que o pente pode aplicar uma força sobre fios individuais de cabelo. Pode-se observar ainda que, uma vez que os fios de cabelo são atraídos para o pente e entram em contacto com este, eles não mais poderão ser atraídos por este.

Parece razoável concluir que a atracção entre o pente e o fio de cabelo é o resultado de alguma entidade física que estaria sendo transferida de um para o outro quando são mutuamente esfregados, com a mesma entidade física sendo transferida de volta para neutralizar a atracção quando estes entram em contacto. Esta entidade física é chamada de carga eléctrica, e actualmente esta transferência é compreendida baseada no facto de que electrões podem ser removidos dos átomos de um objecto e ligados aos átomos de um outro objecto.

A transferência de carga eléctrica através da fricção é um fenómeno frequentemente observado. Quando um raio vence a distância entre uma nuvem e o solo, quando pedaços de âmbar esfregados em camurça podiam atrair partículas de palha, está se observando os efeitos dessa transferência de carga.

Quando um objecto é ‘‘carregado’’ (isto é, quando transfere-se cargas para este), constata-se que este pode exercer uma força em um outro objecto carregado. As primeiras observações de que esta força pode ser tanto atractiva quanto repulsiva conduziram à conclusão de que existiam dois tipos de cargas eléctricas, que foram chamadas de positiva e negativa.

Embora os efeitos resultantes da transferência de carga possam ser poderosos, é notável que esses efeitos são originados da transferência de apenas uma minúscula fracção da carga eléctrica contida nos objectos. É notório que a matéria é composta de átomos electricamente neutros ou moléculas que contém mesmas quantidades de cargas positivas (o núcleo) e cargas negativas (os electrões). Quando dois objectos são esfregados juntos, relativamente poucos electrões dos átomos de um objecto são transferidos para os átomos do outro: a maior parte dos electrões não é afectada. É esta ligeira perturbação no equilíbrio entre a enorme, mas idêntica, quantidade de cargas positivas e negativas em um objecto que é responsável pela maioria dos efeitos eléctricos usuais observados.

Quando se esfrega um bastão plástico em camurça, electrões são transferidos para o bastão: como a camurça tem excesso de electrões (que carregam uma carga negativa), o bastão torna-se negativamente carregado. A camurça agora tem uma deficiência em electrões e, portanto, está carregada positivamente. Pode-se verificar a atracção do bastão sobre fios individuais de camurça, o que é devido à carga que cada fio tem. De maneira semelhante, pode-se esfregar um bastão de vidro na seda e observa-se que ambos tornam-se carregados e podem atrair-se mutuamente. Em cada caso, transferiu-se um número relativamente pequeno de electrões e perturbou-se a neutralidade eléctrica destes objectos.

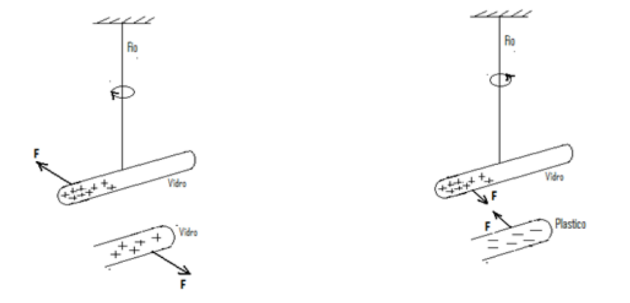
Um bastão de vidro é carregado esfregando-se umas das suas pontas com seda e depois é suspenso por um fio, como mostrado na Fig.1. Ao colocar-se nas proximidades um bastão de vidro carregado com cargas do mesmo sinal verifica-se que os dois bastões repelem-se mutuamente, como mostrado na Fig.1a. Porém, ao posicionar-se um bastão plástico carregado (através da fricção com camurça) nas proximidades, os dois bastões atraem-se mutuamente, como mostrado na Fig.1b.

Fig1(a). Dois bastões carregados com cargas de mesmo sinal repelem-se. Fig1 (b). Dois bastões carregados com cargas de sinais opostos atraem-se.

Explica-se a existência destes dois tipos de forças em função dos dois tipos de cargas. Quando o plástico é esfregado com camurça, electrões são transferidos para o plástico e este torna-se negativamente carregado. Quando o vidro é esfregado com seda, electrões são transferidos para a seda, deixando o vidro com deficiência de electrões e, portanto, com uma carga resultante positiva. As forças observadas na Fig.1 podem ser resumidas pela seguinte regra:
“Carga de mesmo sinal repelem-se mutuamente e cargas de sinais opostos atraem-se mutuamente.”

1.1. QUANTIZAÇÃO DA CARGA ELÉCTRICA

Quando se transfere carga eléctrica de um objecto para um outro, a transferência não pode ser feita em unidades arbitrariamente pequenas. Isto é, o fluxo de cargas como a corrente não é um fluxo contínuo, mas é formado de elementos discretos (individuais). Experiências mostram que a carga eléctrica sempre existe apenas em quantidades que são múltiplos inteiros de determinadas quantidades elementares de carga e. Isto é,
Q  n.e (1) ,

onde:

n  0,1,2,3,….. . n …… número inteiro ;

e  1,6.1019 C ….valor da carga

elementar

A carga elementar e é uma das constantes fundamentais da natureza cujo valor experimental tem sido determinado com uma incerteza de cerca de 4 partes em 108.

O electrão e o protão são exemplos de partículas usuais que têm uma unidade fundamental de carga cada uma. O electrão tem a carga –e, e o protão tem a carga +e. Algumas partículas, como os neutrões, não possuem cargas eléctricas resultantes. Outras partículas elementares conhecidas têm cargas que são múltiplos baixos de e, normalmente ±1, ±2 ou ±3. Cada partícula tem uma anti-partícula correspondente, que tem a mesma massa, mas carga eléctrica de sinal oposto; o anti-electrão, que é conhecido como positrão, tem a carga +e. As partículas não existem normalmente na natureza, mas podem ser criadas através de decaimentos e reacções do núcleo e partículas elementares.

A equação (1) mostra que é possível ter um objecto com carga resultante de + 10e ou – 6e, mas nunca 3,57e.
Quando os valores de uma propriedade são restritos a múltiplos de uma quantidade discreta fundamental, diz-se que esta propriedade é quantizada.

Como a carga elementar é pequena, sobre condições usuais não fica-se ciente da natureza discreta do fluxo de cargas. Por exemplo, em um fio eléctrico de um circuito electrónico em que pequenas correntes de um miliampere são comuns, 6×1015 electrões passam através de qualquer secção transversal do fio eléctrico a cada segundo.

Usualmente, átomos são electricamente neutros, o que significa que estes contêm iguais quantidades de cargas positivas e negativas. O núcleo do átomo contém Z protões (onde Z é chamado de número atómico do átomo) e, desse modo, tem uma carga +Ze. Em um átomo neutro, Z electrões carregados negativamente circulam em volta do núcleo.

Se o átomo não for perturbado e nenhum electrão não for removido, o átomo permanecerá neutro.
A carga eléctrica do protão é igual a carga eléctrica do electrão que designa-se de carga elementar.
e  q  q  1,6.1019 c , e – Quantum de carga ou carga eléctrica
Protão ( p , q  1,6.1019 c ) – tem massa e tem carga
Neutrão ( n , qn  0 ) – não tem carga, tem massa

19
Electrão ( e , qe  1,6.10 c ) – tem massa e tem carga

Unidades de Carga Eléctrica

No sistema internacional ou SI a carga é medida em Coulomb, cujo símbolo é C;
O Coulomb é a quantidade de carga que atravessa em um segundo a secção recta de um fio percorrido por uma corrente constante de um Ampere. Escrevendo este resultado por meio de símbolos, temos: q =it.

No sistema CGS é medida em StatCoulomb, cujo símbolo é StatC.
1C  3.109 StatC

A ilucidação experimental, da quantização da carga eléctrica é feita através da Gota de òleo de Millikan.

As propriedades da carga eléctrica são:
– As cargas não existem de forma independente da matéria (estão associadas a matéria);
– Existem diferentes tipos de substâncias: condutores (cargas móveis) e isoladores (quase não se movem);
– A carga eléctrica pode ser positiva ou negativa (atracção e repulsão);
– A carga eléctrica se conserva;
– A carga eléctrica é quantizada (quantificada);

– A força entre cargas eléctricas puntiformes varia com o inverso do quadrado da distância entre as cargas.

1.2. LEI DE CONSERVAÇÃO DE CARGA ELÉCTRICA
A carga total de um corpo é igual à soma algébrica de todas as cargas eléctricas distribuídas por esse corpo.

‘’ A soma algébrica das cargas eléctricas num sistema fechado mantém-se constante’’.

Um exemplo de conservação da carga é fornecido pelo decaimento radioactivo, do qual um processo típico é:
U238 Th234 + He4
O núcleo radioactivo ‘’pai’’, U238, contém 92 protões (isto é, seu número atómico é Z=92). Ele desintegra-se espontaneamente pela emissão de uma partícula α (núcleo de He4, Z=2), transformando-se no núcleo Th234 com Z = 90. Assim sendo, a quantidade de carga existente (+92e) é a mesma, antes e depois da desintegração.

1.3. CARREGAMENTO POR CONTACTO E POR INDUÇÃO

Suponha que um bastão de vidro positivamente carregado toque um bastão de cobre sem carga (como na Fig.2). Electrões irão fluir do cobre para neutralizar as cargas positivas do vidro. Porém, como os electrões não podem fluir através do vidro, estes podem neutralizar apenas as cargas positivas do ponto de contacto com o cobre. Para transferir electrões adicionais do cobre, pode-se ‘’esfregar’’ o bastão de vidro ao longo do bastão de cobre, transferindo, desse modo, electrões para novas áreas neutras do vidro que entraram em contacto com o cobre (Fig.2a). Removendo-se o bastão de vidro, o cobre permanece com deficiência de electrões e, portanto, com uma carga positiva resultante. Os electrões fluirão através do cobre de forma que as cargas

positivas (os núcleos dos iões) ficam uniformemente distribuídas ao longo da superfície do cobre.

Essa transferência directa de carga de um objecto para outro é chamada de carregamento por contacto. Ainda que electrões negativos sejam de facto transferidos, muitas vezes é conveniente considerar a experiência mostrada na Fig.2 como se as cargas positivas fossem transferidas do bastão de vidro para o cobre.

Fig2(a). Carregando por contacto. Electrões fluem do cobre para neutralizar cargas positivas do ponto de contacto com o vidro. (b). A carga resultante no cobre quando o vidro é removido.

Fig 2’(a) Carregando por indução. Electrões fluem do solo para neutralizar as cargas positivas na ponta mais distante do bastão do cobre. (b) A carga resultante no cobre quando o vidro é removido.

Se um fio for conectado entre a ponta positiva do cobre e o solo (como mostrado na Fig.2a), electrões fluirão do solo para neutralizar as cargas positivas do cobre. Mantendo o bastão de vidro na mesma posição e, em seguida, removendo a conexão com o solo, o bastão de cobre retém a carga negativa resultante. Se então for removido o bastão de vidro, as cargas negativas serão distribuídas sobre a superfície de cobre (Fig.2’b) de forma a ficarem a mais distante possível uma das outras. Esse método de carregar um objecto é chamado de carregamento por indução. Note que um bastão de vidro carregado positivamente tem sido usado para transferir tanto cargas positivas para o cobre por contacto quanto cargas negativas (do solo) por indução.

A separação das cargas positivas e negativas em um objecto isolado (neutro) sob a influência de um objecto próximo carregado é conhecida como polarização.

Fig. O pente carregado negativamente polariza as cargas nas moléculas (do papel), resultando em uma força atractiva entre o pente e o papel.

2. Conceito de Interacção

2.1. Tipos de Interacção Electromagnética

– Interacção Gravitacional (massa);
– Interacção Eléctrica (cargas);
– Interacção Magnética (cargas em movimento);
– Interacção Nuclear Forte (no interior dos protões e neutrões);
– Interacção Nuclear Fraca (processos de decaimento nuclear).

2.1.1. Interacção Gravitacional Força Gravitacional

→
F  G

m1m2 →


G r 2 r

Campo Gravitacional

→
E  FG
G M

m →
r 2 er

Fig. Linhas de força do campo gravitacional.

Energia Potencial Gravitacional

EPG

 G m1m2
r

Potencial Gravitacional

V  EPG
G m

 G m1
r

2.2. Interacção Eléctrica

2.2.1. Força Electrostática. Lei de Coulomb

Até agora, estabeleceu-se que existem dois tipos de cargas eléctricas e que as cargas exercem forças umas nas outras. O objectivo neste momento é entender a natureza desta força.

A primeira experiência quantitativa, bem-sucedida para estudar a força entre as cargas eléctricas foi feita por Charles Augustin Coulomb (1736-1806), que mediu atracções e repulsões eléctricas e deduziu a lei que as rege.

Experiências feitas por Coulomb e seus contemporâneos mostram que a força eléctrica aplicada por um corpo carregado em outro depende directamente do produto das intensidades das duas cargas e inversamente do quadrado de suas distâncias. Isto é,

F r 2

onde F é a intensidade da força mútua que age em cada uma das duas cargas distância entre seus centros.

q1 e

q2 , e r é a

A força em cada carga devido à outra carga actua ao longo de uma linha imaginária que liga as

cargas. Conforme requere a Terceira lei de Newton, a força aplicada de

q1 em q2

é igual em

intensidade, mas de sentido oposto à força aplicada de q2
cargas possam ser diferentes.

em q1 , ainda que as intensidades das

Para tornar a proporcionalidade anterior uma equação, precisa-se inserir uma constante de proporcionalidade K, que é chamada de constante de Coulomb. Deste modo, obtém-se, para forças entre cargas,
F  K
r 2

(1)

A equação (1), que é chamada de lei de Coulomb, é geralmente empregada apenas para objectos carregados cujo tamanho é muito menor que a distância entre estes. Diz-se muitas vezes que esta pode ser empregada apenas para cargas pontuais.

A lei de Coulomb assemelha-se à lei de gravitação de Newton, F = Gm1m2/r2, que já tinha 100 anos na época dos experimentos de Coulomb. Ambas são leis do inverso do quadrado, e a carga q desempenha a mesma função, na lei de Coulomb, que a massa m na lei de gravitação de Newton. Uma diferença entre as duas leis é que as forças gravitacionais são sempre atractivas, enquanto forças electrostáticas podem ser repulsivas ou atractivas, dependendo de as duas cargas terem sinais iguais ou opostos.

No SI, a constante K é explicitada da seguinte forma:

K  1 40
(2)

A constante

 0 , que é chamada de constante eléctrica (também conhecida por permissividade),

tem um valor que é determinado pelo valor da velocidade da luz. Seu valor exacto é 8,85418781762 x 10-12C2/N.m2.

 0 =

A constante de Coulomb K tem um valor correspondente (com três algarismos significativos) a

saber: K 

1
40

 8,99×109 Nm2
C 2

Com esta escolha de constante K, a lei de Coulomb pode ser escrita:
F  1 q1 q2
40 r
(3)

Quando K tem o valor mostrado anteriormente, expressando q em coulombs e r em metros tem- se a força em Newtons.

A importância da lei de Coulomb vai muito além da descrição das forças aplicadas por esferas carregadas uma nas outras. Essa lei, quando unida à estrutura da física quântica, descreve correctamente (1) as forças eléctricas que ligam os electrões de um átomo ao seu núcleo, (2) as forças que ligam átomos entre si para a formação de moléculas e (3) as forças que ligam átomos e moléculas entre si para formar sólidos e líquidos. Deste modo, a maior parte das forças do dia- a-dia que não são gravitacionais em sua essência são eléctricas.

EXEMPLOS

Exemplo.1 Uma moeda de cobre contém tantas cargas positiva quantas cargas negativas, cada uma com intensidade de 1,37 x 105 C. Considere que essas cargas podem ser

concentradas em dois pacotes separados, mantidos afastados por 100m. Que forças atractivas irão agir em cada pacote?

Solução:

Da equação (3) tem-se:

F 
40

(8,99×109 N.m2 / C 2 )(1,37×105 C)2
r 2 (100m)2

= 1,69 x 1016 N

Isto é, cerca de 2 x 1012 toneladas de força. Mesmo que as cargas estivessem separadas pelo diâmetro da Terra, a força atractiva ainda seria de 120 toneladas. Até aqui evitou-se o problema de montar as cargas separadas em forma de ‘’pacote’’ cujas dimensões são pequenas comparadas com sua separação. Tais pacotes, se pudessem ser formados, explodiriam em pedaços pela força de repulsão mútua de Coulomb.

A lição desse problema resolvido é que não se pode perturbar muito a neutralidade eléctrica da material. Ao tentar-se tirar uma fracção de tamanho considerável da carga existente em um corpo, uma grande força de Coulomb surge automaticamente, tendendo a trazê-la de volta.

Exemplo.2. A distância média r entre um electrão e um protão em um átomo de hidrogénio é de 5,3×10-11 m. (a) Qual o valor médio da força electrostática que age entre essas partículas? (b) Qual a intensidade média da força gravitacional que age entre essas partículas?

Solução: (a)

Da equação (3) tem-se:

F  1
e 4

e2 
r 2

(8,99×109 N.m / C 2 )(1,60×1019 C)2
(5,3×1011m)2

= 8,2 x 10-8N.

Embora essa força possa parecer pequena (esta é em torno do peso de uma partícula de poeira), produz uma imensa aceleração do electrão dentro dos limites do àtomo, em torno de 1023 m/s2.

(b) Para a força gravitacional, tem-se:
F  G memp 
g r 2
 (6,67×1011 N.m2 / kg2 )(9,11×1031kg)(1,67×1027 kg) (5,3×1011m)2
 3,6×1047 N

Observa-se que a força gravitacional é mais fraca que a força electrostática por um factor em torno de 1039. Embora a força gravitacional seja fraca, esta é sempre atractiva. Deste modo, ela pode agir na formação de massas muito grandes, como aquelas existentes na formação de estrelas e galáxias, de forma que grandes forças gravitacionais podem se desenvolver.

A força electrostática, por outro lado, é repulsiva para cargas do mesmo sinal, desse modo, não se pode acumular grandes concentrações tanto de cargas positivas quanto de cargas negativas. Sempre existem dois tipos de carga simultaneamente, compensando-se umas às outras. As cargas que costumam-se observar nas experiências do dia-a-dia são ligeiras perturbações deste equilíbrio nulo.

Exemplo.3. O núcleo de um àtomo de ferro tem um raio de cerca de 4×10-15m e contém 26 protões. Que força repulsiva electrostática age entre dois protões neste núcleo se estão separados pela distância de um raio?
Solução:
Da equação (3) tem-se:

F  1 e
40 r

 (8,99×109 N.m2 / C 2 )(1,60×1019 C)2
(4×1015 m)2

 14N.

A grande força electrostática repulsiva, em torno de 14N, que age sobre um único protão, precisa ser contrabalançada por uma força nuclear atractiva que mantém o núcleo coeso. Essa força, cujo

alcance é tão pequeno que seus efeitos quase não podem ser sentidos fora do núcleo, é conhecida
como ‘’força nuclear forte’’ e é bem merecida essa denominação.

2.2.2. Lei de Coulomb na Forma Vectorial

Até este ponto considerou-se apenas a intensidade da força exercida de uma carga em outra, determinada de acordo com a lei de Coulomb. A força, sendo um vector, possui também propriedades direccionais. No caso da lei de Coulomb, o sentido da força é determinado pelo sinal relativo das duas cargas eléctricas.

Conforme ilustrado na figura que se segue, considere que existam duas cargas pontuais q1 e q2
separadas pela distância r12. Inicialmente, supõe-se que as cargas têm o mesmo sinal e, portanto, repelem-se mutuamente. Considere a força sobre a partícula 1 aplicada pela partícula 2, que pode
→
ser escrita na sua forma usual como F12 . O vector posição que situa a partícula 1 em relação à

partícula 2 é

→ , isto é, definindo-se a origem do sistema de coordenadas na posição da partícula

2, então

→ será o vector posição da partícula 1.

Fig.3. Carga q1

na posição →

→
e carga q2 na posição r2

em relação à origem O. A força exercida por

→ → → →

q1 sobre q2,

F21

está na direcção do vector

r12  r2  r1

quando as duas cargas têm o mesmo

sinal, e na direcção oposta quando as cargas têm sinais opostos.

Se duas cargas têm o mesmo sinal, então a força é repulsiva e, como mostrado na figura 3(a),

→
F12

deve ser paralelo a
→

→ . Se as cargas tiverem sinais opostos, como na figura 3(b), então a força
→

F12 é atractiva e tem a mesma direcção, mas sentido contrário que

r12 .

Nos dois casos, pode-se representar a força como:

→  1

q1q2 rˆ

F12

40
(4)

12
12

Fig.3 (a). Duas cargas pontuais q1 e q2 de mesmo sinal aplicam forças repulsivas de módulos iguais e sentidos opostos uma na outra. O vector posiciona q1 em relação a q2, e o vector unitário aponta no sentido de . Observe que é paralelo a . (b)As duas cargas têm agora sinais opostos, e a força é atractiva. Note que está no sentido contrário em relação a .

Neste caso, o r é a intensidade do vector

→ , e rˆ

representa o vector unitário no sentido de → .

12

Isto é,
→

r12 12

r12

rˆ12

 r12
r12

(5)
→

De acordo com a terceira lei de Newton, a força aplicada na partícula 2 pela partícula 1 é
→

F21 ,

tem o sentido oposto a

F12 . Esta força pode então ser explicitada exactamente da mesma forma:

→  1

q1q2 rˆ

F21

4

r 2 21

0 21
(6)

onde

rˆ21 é um vector unitário que aponta da partícula 1 para a partícula 2, isto é, seria o vector

unitário no sentido da partícula 2 se a origem do sistema de coordenadas estivesse na posição da partícula 1.

2.3. Superposição da Força Eléctrica

A representação vectorial da lei de Coulomb é útil porque carrega consigo a informação
→
direccional sobre F e se a força é atractiva ou repulsiva. Usar a representação vectorial é de
grande importância ao considerarem-se forças agindo em um conjunto de mais de duas cargas.

Nesse caso emprega-se a equação (4) para cada um dos pares de cargas e encontra-se a força total em qualquer carga através da utilização da soma vectorial das forças devidas a cada uma das outras cargas.
Por exemplo, a força sobre a partícula 1 em um conjunto seria:
→ → → →
F1  F12  F13  F14  ,
(7)
→ →

onde

F12

é a força exercida sobre a partícula 1 pela partícula 2,

F13

é a força exercida sobre a

partícula 1 pela partícula 3, e assim por diante.

A equação (7) é a representação matemática do princípio de superposição empregado para forças eléctricas. Este princípio afirma que:

‘’A força agindo em uma carga devido a outra é independente da presença de outras cargas e, portanto, pode-se calcular separadamente a força para cada par de cargas e então utilizar a soma vectorial para encontrar-se a força resultante em qualquer carga’’.

Por exemplo, a força

→
F13

que a partícula 3 aplica sobre a partícula 1 não é de forma alguma

afectada pela presença da partícula 2.

Fig.3 (c). A força exercida pelas cargas q1 e q2 sobre a carga q3 é igual a soma vectorial das forças resultantes criadas pelas duas cargas sobre q3.

Exemplo 4: A figura ao lado mostra três partículas carregadas, mantidas em posição por forças não mostradas. Qual é a força electrostática, devido às duas outras cargas, que age a carga q1 ? Seja: q1 = – 1,2µC, q2 = + 3,7 µC, q3 = – 2,3 µC, r12 = 15 cm, r13 = 10 cm e θ = 32o.

Fig 4. Na figura do problema 4 as três cargas aplicam três pares de forças de acção reacção umas nas outras. Apenas as duas forças que agem em q1 são mostradas.

Solução:

Aplicando o princípio de superposição teremos que:

Calculam-se primeiro as intensidades das forças que q2 e q3 aplicam sobre q1. Substituindo as intensidade das cargas na equação (3) tem-se:

1 q1 q2

(8,99×109 N.m2 / C 2 )(1,2×106 C)(3,7×106 C)

F12  4 2

(0,15m)2

 1,77N

As cargas q1 e q2 têm sinais opostos, e assim, a força aplicada por q2 em q1 é atractiva. Em
→
consequência, F12 aponta para a direita de acordo com a figura.

Também para

→
F13 tem-se:

F13 

(8,99×109 N.m2 / C 2 )(1,2×106 C)(2,3×106 C) (0,10m)2

 2,48N

Essas duas cargas têm o mesmo sinal (negativo), assim a força aplicada por q3 sobre q1 é
→
repulsiva. Em consequência F13 aponta como mostra a figura do exercício.

As componentes da força resultante correspondentes da equação (7), ou,

→
F1 aplicada sobre q1 são determinadas pelas componentes

F1x  F12 x  F13x  F12  F13 sen 
 1,77N  (2,48N )(sen32o )  3,08N
e

F1y  F12 y  F13 y

 0  F13 cos 

 (2,48N )(cos32o )  2,10N
Destas componentes, pode-se mostrar que a intensidade (módulo) de vector forma um ângulo de – 34o com o eixo X.

2.4. DISTRIBUIÇÃO CONTÍNUA DAS CARGAS

→
F1 é 3,73N e que esse

Até esse ponto viu-se como calcular as forças devidas a cargas pontuais. Em muitos casos, no entanto, as forças eléctricas são aplicadas por objectos carregados com forma de bastões, placas, ou sólidos. Por simplicidade, supõem-se que os objectos são isoladores e que a carga distribui-se por toda a superfície ou volume do objecto, formando uma distribuição de carga contínua.

A figura (2) mostrou as forças aplicadas por um bastão carregado em outro. A lei de Coulomb se aplica apenas a cargas pontuais e, portanto, não se pode usar a lei de Coulomb na sua forma para cargas pontuais para calcular a força aplicada por um bastão carregado em outro. É possível imaginar os bastões cobertos com cargas pontuais e utilizar-se a lei de Coulomb para calcular a força aplicada por cada carga pontual de um bastão em cada carga pontual do outro bastão, mas tal abordagem seria desesperadamente complexa — se os bastões tivessem uma pequena carga de apenas 1nC, seria necessário considerar 1010 cargas pontuais em cada bastão.

Em vez disso, volta-se à ideia da época de Franklin e considera-se a carga como uma propriedade contínua. O procedimento básico é dividir a carga em elementos infinitesimais e utilizar métodos de cálculo para achar a força total devida a todos os elementos.

Se um objecto contém uma carga resultante q, pode-se imaginar que esta possa ser dividida em muitos pequenos elementos dq. Cada elemento tem um certo comprimento, área, ou volume, dependendo se são consideradas cargas que estão distribuídas respectivamente em uma, duas, ou três dimensões. Pode-se expressar dq em termos do tamanho do elemento e da densidade de carga, que descreve como as cargas são distribuídas ao longo do comprimento, área, ou volume do objecto. Para a maioria dos problemas considerados neste texto, as cargas serão distribuídas uniformemente sobre o objecto, o que significa que a densidade de carga tem o mesmo valor em qualquer ponto do objecto.

Em algumas circunstâncias, as cargas são distribuídas em uma dimensão, como nos bastões delgados da Fig (2). Nesse caso, pode-se explicitar dq em termos de densidade linear de carga (carga por unidade de comprimento) λ, cuja unidade básica é C/m. Um pequeno elemento do bastão de comprimento dx tem carga dq dada por:

dq = λdx
(8)

Se o bastão é uniformemente carregado, de forma que a carga total q é espalhada uniformemente por todo o comprimento L, então λ = q/L. Por exemplo, um bastão de comprimento L = 0,12m com carga uniformemente distribuída de q = 5,4×10-6C tem uma densidade linear de carga λ = q/L = 4,5×10-5C/m. Um pedaço curto do bastão com comprimento dx = 1,0mm teria dq = λdx = 4,5×10-8 C.

Em outras situações, cargas poderiam distribuir-se sobre uma área bidimensional, como a superfície de partículas esféricas condutoras. Nesse caso, dq é explicitado em termos de densidade superficial de carga (carga por unidade de área) σ, medida em unidades do SI de C/ m2 . Um pequeno elemento de área dA teria a carga expressa por:
dq = σ/dA (9)

Se a carga q é distribuída uniformemente sobre a superfície de área A, então σ = q/A.

A carga também pode ser espalhada completamente pelo volume de um objecto tridimensional. Neste caso, utiliza-se densidade volumétrica de carga (carga por unidade de volume) ρ, cuja unidade do SI é C/m3. A carga dq em um elemento de volume dV será então:

dq = ρdV (10)

Se a carga q é distribuída uniformemente por todo o volume V, então ρ= q/V.

Para ilustrar esses conceitos, calcula-se as expressões das forças aplicadas por uma distribuição contínua de cargas sobre uma carga pontual qo. Pela extensão destes métodos, é possível calcular a força aplicada por uma distribuição contínua de carga em outra.
O procedimento para encontrar-se a força aplicada por uma distribuição contínua de cargas sobre uma carga pontual é visto a seguir:
1. Suponha que uma distribuição contínua de cargas seja dividida em um grande número de pequenos elementos de carga.
2. Seleccione um elemento de carga arbitrário e explicite a sua carga dq em termos das equações (8), (9) e (10), dependendo de a carga ser distribuída sobre uma linha, uma área, ou um volume, respectivamente.
3. Uma vez que dq é infinitamente pequeno, pode-se considerar como se fosse uma carga pontual. Explicita-se a intensidade do elemento de força dF aplicado pela carga dq na carga qo em termos da lei de Coulomb, equação (3):

dF  1 dq qo

4o r

(11)

onde r é a distância entre dq e qo.

4. Levando-se em conta os sinais e posições de dq e qo, determina-se a direcção e o sentido do elemento de força dF.
5. Determina-se então a força total pela soma de todos os elementos de força infinitesimais, que implica na integral:

→ →
F   dF
(12)

Ao efectuar essa integral, normalmente precisa-se levar em conta que diferentes elementos de
→
carga dq podem prover elementos de força dF em direcções e sentidos distintos. A equação
→
(12) representa na realidade três componentes de F :

Fx   dFx

, Fy   dFy

, Fz   dFz

(13)

Ocasionalmente pode-se utilizar argumentos baseados em simetria para evitar o cálculo de uma ou duas dessas integrais.

2.4.1. UMA LINHA DE CARGA UNIFORME
Na figura a seguir mostra-se um bastão delgado de comprimento L que encontra-se alinhado com o eixo z e que possui cargas positivas uniformemente distribuídas q, de forma que a densidade

linear de cargas é

  q L . Necessita-se determinar a força aplicada pelo bastão em uma carga

pontual qo, posicionada na perpendicular à linha divisora do bastão (a parte positiva do eixo y) a uma distância y de seu centro.

Fig 5. Bastão uniformemente carregado. Para achar a força na carga pontual q0, considera-se que o bastão seja constituído por vários elementos individuais de carga como a dq.

Suponha que o bastão seja dividido em pequenos elementos de comprimento dz. Um elemento

arbitrário de carga sobre qo, onde:

dq  dz

é posicionado a uma distância z de seu centro e aplica a força dF

dF 

1
40

q0 dq .
r 2

A direcção e o sentido da força

→
dF são mostrados na figura. Não há componente

→
dF na direcção

x (perpendicular à página), então Fx = 0. Pode-se inclusive utilizar argumentos de simetria para mostrar que Fz = 0. Para cada elemento de carga dq na posição + z, existe um outro elemento de carga posicionado em – z. Quando somam-se as forças devidas a elementos de carga em + z e – z, obtém-se que as componentes em z têm intensidades iguais, mas apontam em sentidos opostos, desse modo a sua soma é nula.

Como a carga q0 é posicionada no plano médio do bastão, esse cancelamento irá ocorrer para cada par de elementos de carga ao longo de todo o comprimento do bastão. Conclui-se, portanto, que Fz = 0. Apenas

Fy resta para ser cancelada. O elemento

dFy  dF cos 

é mostrado na figura.

Com dq  dz , r 2  y2  z2 , e cos 

, tem-se:

dFy

 dF cos 

1
40

q0dq cos  1
r 2

q0dz y

F  dF  1 q y
0

L / 2

L / 2

dz

y2  z2 3/ 2

Fy 

q0q

Calculando-se a integral, obtém-se:

Fy 

q0q

2.4.2. UM ANEL DE CARGAS

A figura a seguir mostra um anel delgado de cargas de raio R com carga q positiva

uniformemente distribuída, de forma que a sua densidade linear é

  q 2R . Deseja-se achar a

força aplicada pelo anel sobre uma carga pontual positiva q0 posicionada no eixo do anel (que escolhe-se como a parte positiva do eixo z) a uma distância z do centro do anel.

Fig. Um anel carregado uniformemente. Para achar a força em uma carga pontual q0, considera- se que o anel consiste de vários elementos individuais de carga como dq.

Um pequeno elemento de carga do anel tem comprimento
dq  Rd .

A força dF aplicada sobre q0 por dq é:

Rd

e, deste modo, tem uma carga

dF 

1
40

q0 dq 
r 2

1
40

q0Rd
z 2  R2 

→
Pode-se usar argumentos de simetria para estabelecer que a única componente não nula de F é a
componente em z. Para cada elemento dq do anel, existirá um outro elemento de mesma carga dq do lado oposto do diâmetro através do centro do anel; quando os elementos de carga são somados, todas as outras componentes de forças que não as Fz serão canceladas. Com

cos 

, acha-se:

Fz   dFz   dF cos
  1 q0Rd z
1 q Rz 2

0
3/ 2

 d

40 z 2  R2  0

A integral calculada ao longo do anel resulta em 2

e , portanto, o resultado final para força é:

Fz 

1
40

q0 qz
z 2  R2 3/ 2

2.4.3. UM DISCO DE CARGAS

A figura a seguir mostra um disco circular de raio R que tem carga positiva q distribuída

uniformemente por toda a superfície, assim, a densidade superficial de carga é   2 . Uma

carga pontual positiva q0 é posicionada no eixo do disco ( parte positiva do eixo z) a uma distância z do eixo do disco.

Fig 6. Um disco circular que tem uma densidade superficial de carga uniforme. A força em uma carga pontual q0 é determinada pela divisão do disco em anéis circulares delgados.

Para determinar a força aplicada pelo disco sobre a carga pontual, pode-se dividir o disco em uma série de anéis concêntricos. A carga em um anel de raio w e espessura dw na figura é dq  dA   (2wdw)  2wdw .

A força

dFz

aplicada sobre a carga q0 por esse anel pode ser determinada utilizando-se a

equação

Fz 

1
40

q0 qz
z 2  R2 3/ 2

, substituindo-se q por dq e R por w, logo surge:

dFz

 1 40

q (2wdw)z z 2  R2 3/ 2

Para somar os elementos de força devidos a todos os anéis, integra-se w variando de 0 a R:

1 R wdw

Fz  4

q0 2z z 2  R2 3/ 2

1 2q0q  z 

 1 

40 

z 2  R2 